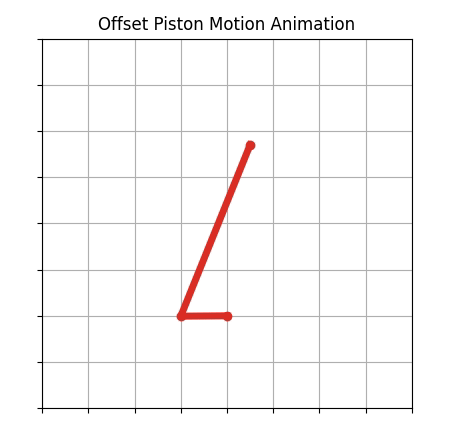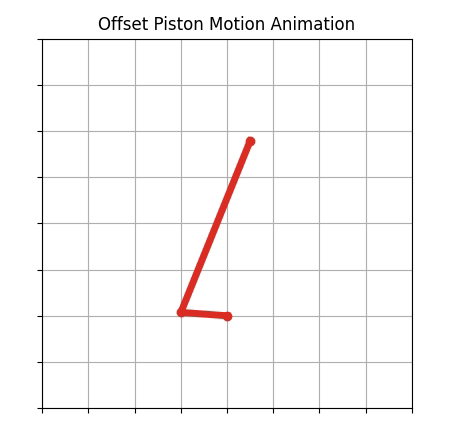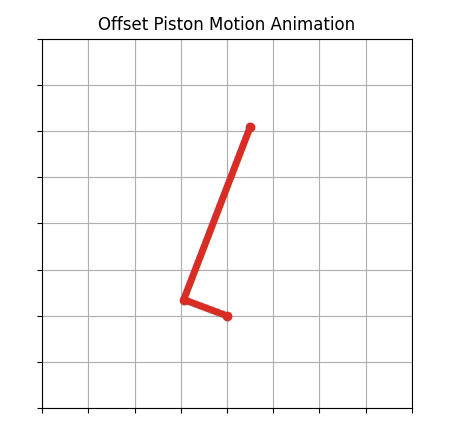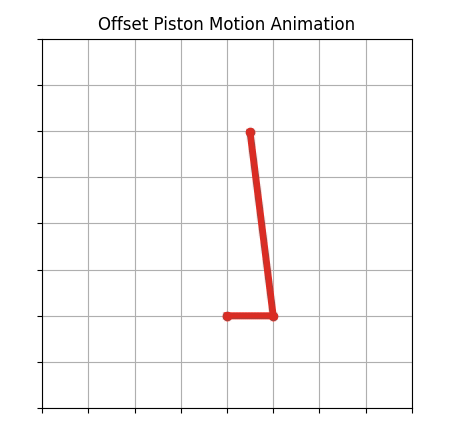
Offset Piston Motion with Python and Matplotlib

Offset piston motion is one of the classic types of engineering dynamics motion that belong to a category of 4-bar motion. Piston motion is the type of motion that the piston in a cylinder of a car engine goes through as the crankshaft rotates.

Offset piston motion has the same type of motion, but the centerline of the piston is not in line with the center of the crankshaft.

This type of offset piston/crankshaft geometry is sometimes used in automobile engines. For example, some Toyota automobile engines have an offset piston geometry.

Set up a Python virtual environment

To start this process, we will set up a Python virtual environment.

Real Python has a good introduction to virtual environments and why to use them.

Windows 10

I use Windows 10 and the Anaconda distribution of Python. Virtual environments can be created on Windows 10 using the Anaconda Prompt

Type into the Anaconda Prompt on Windows:

> conda create -y -n offset_piston_motion python=3.7

MacOS or Linux

If you are using MacOS or Linux, a terminal can be used to create a Python virtual environment.

Type into a terminal on MacOS or Linux:

$ mkdir offset_piston_motion
$ cd offset_piston_motion
$ python3 -m venv venv

Install Python packages

Now that we have a new clean virtual environment with Python 3 installed, we need to install a couple of Python packages: Matplotlib and NumPy. Before the Python packages are installed, we have to make sure that the virtual environment we just created is active. The active virtual environment is the virtual environment the packages will be installed into.

Windows 10

On Windows 10, where the virtual environment was created with conda and the Anaconda Prompt, type the commands below to install the necessary packages.

> conda activate offset_piston_motion
(offset_piston_motion) > conda install -y numpy matplotlib

MacOS and Linux

On MacOS or Linux, the command to activate the virtual environment is a little different. Also, on MacOS and Linux, you can use the Python package manager pip to install the Python packages (on Windows, I recommend using conda to install packages)

$ source venv/bin/activate
(venv) $ pip install numpy matplotlib

Start the script with imports

Open a text editor (like VS Code or PyCharm) and create a new Python file called offset_piston_motion.py

At the top of the offset_piston_motion.py script, we'll start by importing the necessary modules. In this section of code, we import NumPy as np and also import a couple of trig functions from NumPy. We will use NumPy's trig functions (instead of the trig functions in Python's Standard Library math module) because the trig functions need to operate on arrays of numbers. From Matplotlib, a Python plotting library, we'll import the pyplot and animation modules.

# import the necessary packages
import numpy as np
from numpy import pi, sin, cos, sqrt
import matplotlib.pyplot as plt
import matplotlib.animation as animation

Initial Parameters

To model offset piston motion we need to have two moving parts: a crankshaft and a connecting rod.

The crankshaft rotates around a central axis with a constant radius. We'll model this rotation with a line of constant length, one end fixed at the origin and the other rotating in a circle like a hand on a clock. To model this crankshaft line, we just need two points, the origin at x=0 and y=0 and the end of the line at the point x1 and y1.

We also need to define a crank radius and a connecting rode length. To ensure the animation does not run indefinitely, we will set a fixed number of rotations. The rotation increment defines how fine the 'ticks' there are as our crankshaft arm rotates. A rotation increment of 0.1 works to make our animation run smoothly enough.

For offset piston motion (compared to regular piston motion), one last parameter we need to define is the offset distance. The offset distance is the horizontal distance between the vertical line that goes through the center of the crankshaft and the vertical line that goes through the end of the connecting rod. In regular piston motion, the offset distance is zero. In offset piston motion, this offset distance is non-negative.

# input parameters
r = 1.0  # crank radius
l = 4.0  # connecting rod length
d = 0.5  # offset distance
rot_num = 6 # number of crank rotations
increment = 0.1 # angle incremement

Create arrays of angles and points

Next, we will create a couple of arrays of angles and points. NumPy's np.arange() optionally accepts three arguments (start,stop,step). Note that the stop value is not included in the array, so we append our stop value onto the end of the angles array with NumPy's np.append() function.

After the angles are defined, we create a couple of arrays that contain zeros (the zeros are just place holders) and are the same length as the angles array.

# create the angle array, where the last angle is the number of rotations*2*pi
angle_minus_last = np.arange(0,rot_num*2*pi,increment)
angles = np.append(angle_minus_last, rot_num*2*pi)

X1=np.zeros(len(angles)) # crank x-positions: Point 1
Y1=np.zeros(len(angles)) # crank y-positions: Point 1
X2=np.zeros(len(angles)) # connecting rod x-positions: Point 2
Y2=np.zeros(len(angles)) # connecting rod y-positions: Point 2

Loop through angles

After the angles array is defined, we can loop through the angles and define points that define the location of the end of the crankshaft and the end of the connecting rod.

To keep track of the number of times through the loop, we'll use Python's enumerate() function. Note that enumerate() can output two values, the index and the iterable (in this case the iterable is the angle theta from the `angles array).

# calculate the crank and connecting rod positions for each angle
for index,theta in enumerate(angles, start=0):
    x1 = r*cos(theta) # x-cooridnate of the crank: Point 1
    y1 = r*sin(theta) # y-cooridnate of the crank: Point 1
    x2 = d # x-coordinate of the rod: Point 2
    y2 = r*sin(theta) + sqrt(l**2 - (r*cos(theta)-d)**2) # y-coordinate of the rod: Point 2
    X1[index]=x1 # crankshaft x-position
    Y1[index]=y1 # crankshaft y-position
    X2[index]=x2 # connecting rod x-position
    Y2[index]=y2 # connecting rod y-position

Create the Matplotlib figure and plot

Now that the point arrays are all defined, we can set up our Matplotlib figure window and add a subplot to it. Note how the aspect='equal' is supplied as an input argument. If aspect='equal' is not set, the crankshaft will look like it rotates around in an oval.

# set up the figure and subplot
fig = plt.figure()
fig.canvas.set_window_title('Matplotlib Animation')
ax = fig.add_subplot(111, aspect='equal', autoscale_on=False, xlim=(-4,4), ylim=(-2,6))
ax.grid()
ax.set_title('Offset Piston Motion Animation')
ax.axes.xaxis.set_ticklabels([])
ax.axes.yaxis.set_ticklabels([])
line, = ax.plot([], [], 'o-', lw=5, color='#de2d26')

Initialization function

Next, we'll define an initialization function. An initialization function is needed to make the animation work.

# initialization function
def init():
    line.set_data([], [])
    return line,

Animation function

A second function we need to define is an animation function.

# animation function
def animate(i):
    x_points = [0, X1[i], X2[i]]
    y_points = [0, Y1[i], Y2[i]]
    line.set_data(x_points, y_points)
    return line,

Call the animation and show the plot

The offset_piston_motion.py script is almost finished. All have left to do is call our animation and show the plot.

# call the animation
ani = animation.FuncAnimation(fig, animate, init_func=init, frames=len(X1), interval=40, blit=True, repeat=False)
## to save animation, uncomment the line below:
## ani.save('offset_piston_motion_animation.mp4', fps=30, extra_args=['-vcodec', 'libx264'])

# show the animation
plt.show()

Run the script

After the offset_piston_motion.py script is complete and saved, the script can be run from the Anaconda Prompt (on Windows 10) or a terminal (On MacOS or Linux). Make sure the virtual environment we created earlier is active before running the script.

> python offset_piston_motion.py

The resulting animation

A video of the resulting animation is shown below:

The complete code

The complete offset_piston_motion.py script is shown below. You can also find the code on GitHub here

# offset_piston_motion.py
"""
Offset Piston Motion Animation using Matplotlib
Author: Peter D. Kazarinoff, 2021
MIT License
"""

# import the necessary packages
import numpy as np
from numpy import pi, sin, cos, sqrt
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# input parameters
r = 1.0  # crank radius
l = 4.0  # connecting rod length
d = 0.5  # offset distance
rot_num = 6 # number of crank rotations
increment = 0.1 # angle incremement

# create the angle array, where the last angle is the number of rotations*2*pi
angle_minus_last = np.arange(0,rot_num*2*pi,increment)
angles = np.append(angle_minus_last, rot_num*2*pi)

X1=np.zeros(len(angles)) # crank x-positions: Point 1
Y1=np.zeros(len(angles)) # crank y-positions: Point 1
X2=np.zeros(len(angles)) # connecting rod x-positions: Point 2
Y2=np.zeros(len(angles)) # connecting rod y-positions: Point 2

# calculate the crank and connecting rod positions for each angle
for index,theta in enumerate(angles, start=0):
    x1 = r*cos(theta) # x-cooridnate of the crank: Point 1
    y1 = r*sin(theta) # y-cooridnate of the crank: Point 1
    x2 = d # x-coordinate of the rod: Point 2
    y2 = r*sin(theta) + sqrt(l**2 - (r*cos(theta)-d)**2) # y-coordinate of the rod: Point 2
    X1[index]=x1 # crankshaft x-position
    Y1[index]=y1 # crankshaft y-position
    X2[index]=x2 # connecting rod x-position
    Y2[index]=y2 # connecting rod y-position

# set up the figure and subplot
fig = plt.figure()
fig.canvas.set_window_title('Matplotlib Animation')
ax = fig.add_subplot(111, aspect='equal', autoscale_on=False, xlim=(-4,4), ylim=(-2,6))
ax.grid()
ax.set_title('Offset Piston Motion Animation')
ax.axes.xaxis.set_ticklabels([])
ax.axes.yaxis.set_ticklabels([])
line, = ax.plot([], [], 'o-', lw=5, color='#de2d26')


# initialization function
def init():
    line.set_data([], [])
    return line,


# animation function
def animate(i):
    x_points = [0, X1[i], X2[i]]
    y_points = [0, Y1[i], Y2[i]]
    line.set_data(x_points, y_points)
    return line,


# call the animation
ani = animation.FuncAnimation(fig, animate, init_func=init, frames=len(X1), interval=40, blit=True, repeat=False)
## to save animation, uncomment the line below:
## ani.save('offset_piston_motion_animation.mp4', fps=30, extra_args=['-vcodec', 'libx264'])

# show the animation
plt.show()