
In this post, we will complete a problem that might come up in a Strength of Materials class. We'll estimate the deflection of a truncated cone given an applied load using Python.
The Problem¶
Below is an engineering mechanics problem that can be solved in Python. Follow along this post to see how to solve the problem with code.
Given:¶
A solid truncated cone is subjected to an axial force $P$ as shown below.
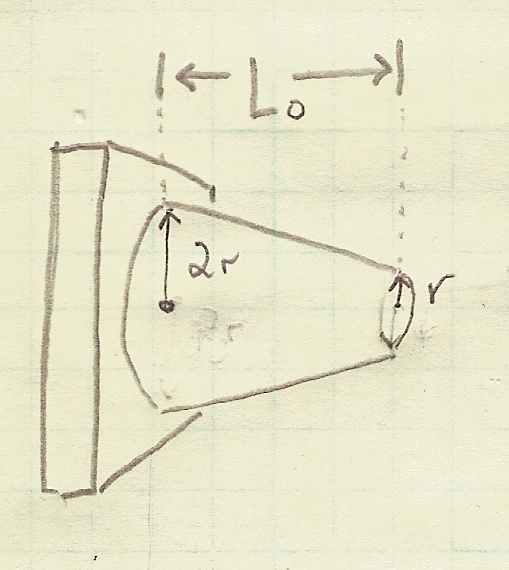
When load $P$ is applied to the cone, the exact elongation, $\delta$ is:
$$ \delta = \frac{PL}{2\pi c^{2}E} $$Find:¶
By replacing the cone by $n$ circular cylinders of equal thickness, determine the elongation of the the truncated cone. Also calculate the percent error obtained from using $n=6$, $n=12$, and $n=60$ circular cylinders.
Assumptions:¶
This problem can be completed generally, but for this solution, we are going to assume the following:
load $P=10 \ MPa$
minor radius $c=5 \ mm$
major radius $2c=10 \ mm$
length $L=100 \ mm$
Elastic Modulus $E=120 \ GPa$
Start the solution: install Python¶
We are going to use Python to code the solution to this problem. If you don't already have Python installed on your computer, I recommend installing the Anaconda distribution of Python. See this post to learn how to install Anaconda on your computer.
I am coding this solution in a Jupyter Notebook. Once you install Anaconda, you can open a Jupyter notebook from the Windows Start Menu or the Anaconda Prompt. See this post to learn about the ways to open a Jupyter notebook.
Alternatively, instead of using a Jupyter notebook, you could code your solution in a .py file.
Alright. Let's get coding....
Calculate the exact value of the deflection of the truncated cone¶
Using the equation for the exact elongation, ($\delta$) above and the assumed values for $P$, $c$, $L$, and $E$, we can calculate $\delta$, which we will call d_exact.
The equation and assumed values are below.
$$ \delta = \frac{PL}{2\pi c^{2}E} $$$P=10 \ MPa$
$c=5 \ mm$
$L=100 \ mm$
$E=120 \ GPa$
To code this solution in Python, first we need to import the math module. From the math module we will use math.pi as our value for $\pi$. We can print our calculated d_exact using a Python f-string. Python f-strings allow us to put variables on the inside of print statements. Variables inside Python f-strings need to be surrounded by curly braces { }. Make sure to pre-pend the f-string with the letter "f".
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
d_exact = (P*L)/(2*math.pi*(c**2)*E)
print(f"The exact value for delfection of the cone is d_exact = {d_exact}")
Model a truncated cone as a series of disks¶
Next we'll see how the approximations of the elongation of the cone compare to the exact elongation d_exact calculated above. We'll calculate the approximate elongation by dividing the cone into separate "disks". Below is a picture of a children's toy to illustrate the concept of modeling a truncated cone as a set of stacked disks. In the picture below, the truncated cone is modeled as 5 disks stacked on top of each other.

The elongation $\delta$ of each "disk" is equal to:
$$ \delta = \frac{PL}{AE} $$where
$\delta$ = deformation, or change in thickness of the disk
$P$ = load
$L$ = original length or thickness of the disk
$A$ = cross-sectional area of the disk
$E$ = elastic modulus (a material property)
We can plot the upper surface of our truncated cone in two dimensions. The x-axis on the plot is the cone length $L$ and the y-axis on the plot is the cone radius $r$. The resulting plot looks like the hand-drawn plot below.
According to our assumed parameters $r = c = 5 \ mm$, $2r = 2c = 10 \ mm$, and $L_0 = 100 \ mm$.
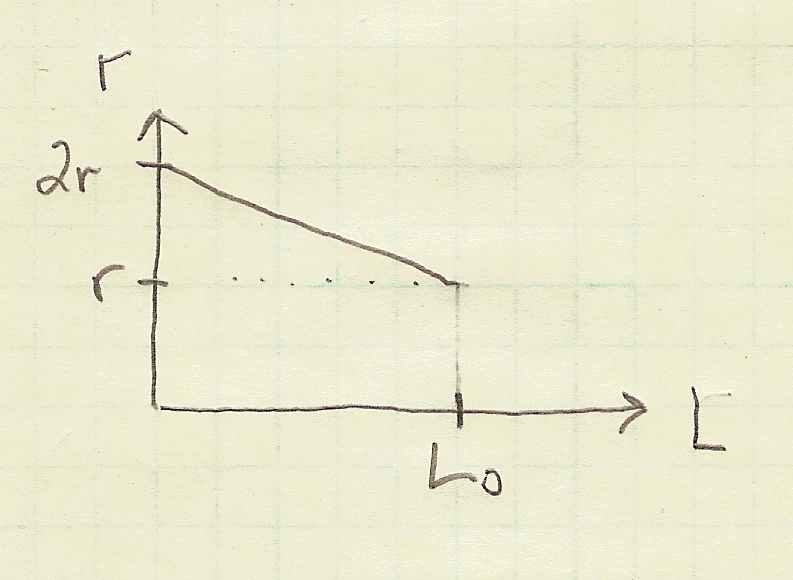
OK. Let's make our first approximation for the deflection of the truncated cone.
Approximate the truncated cone as one disk¶
If the truncated cone is modeled as a single disk (something that kind of looks like a can of soup), the radius of that single disk should be the average of the minor radius $r = 5 \ mm$ and the major radius $2r = 10 \ mm$. The plot below shows this approximation. Note how the upper surface of the cone (the line on the plot) has been approximated as a single horizontal line at a value of $r = 7.5 \ mm$ (the average of $5$ and $10$).
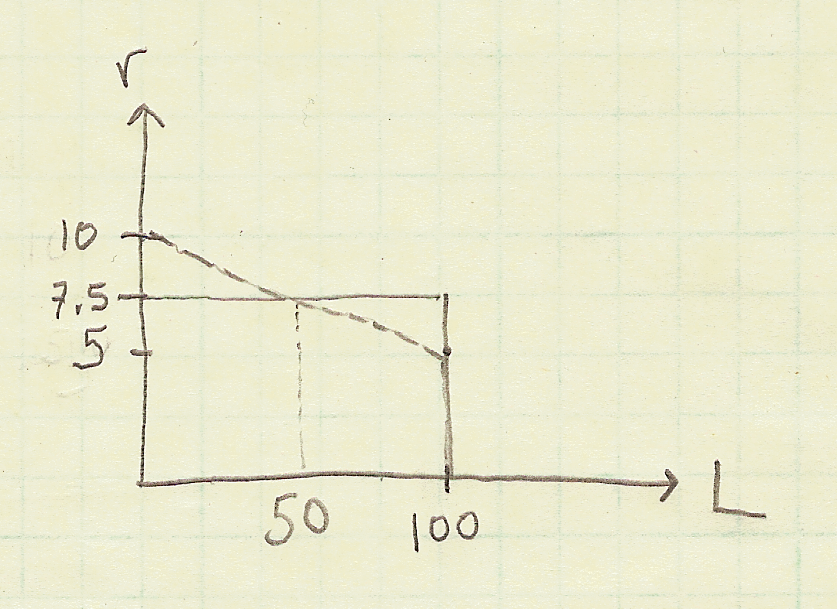
We can calculate the the elongation of this single cylinder (single disk) which has a radius of $r = 7.5$ using the standard equation for elongation in engineering mechanics.
$$ \delta_1 = \frac{PL}{A_{1}E} $$$\delta_1$ = deformation, or change in thickness of the one disk
$P = 10 \ MPa$
$r_1 =7.5 \ mm$ (radius of the one disk)
$A_1 = \pi r^2$ (area of the one disk)
$L = 100 \ mm$
$E = 120 \ GPa$
Let's code this approximation of the elongation (modeling the truncated cone as a single thick disk) in Python.
import math
P = 10
r_1 = 7.5
A_1 = math.pi*r_1**2
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
d_1 = (P*L)/(A_1*E)
print(f"The approximate value for delfection of the cone modeled as one disk is d_1 = {d_1}")
The approximate value calculated value of d_1 is around $4.72 \times 10^{-5}$. This approximate value is in the same order of magnitude as the previously calculated exact value of deflection d_exact which was about $5.31 \times 10^{-5}$.
Approximate the deflection of the truncated cone by modeling it as multiple disks¶
We can more closely approximate the deformation of our truncated cone by dividing the cone into more numerous and successively thinner disks. The plot below shows the progression of using two disks, then three disks, then four disks.
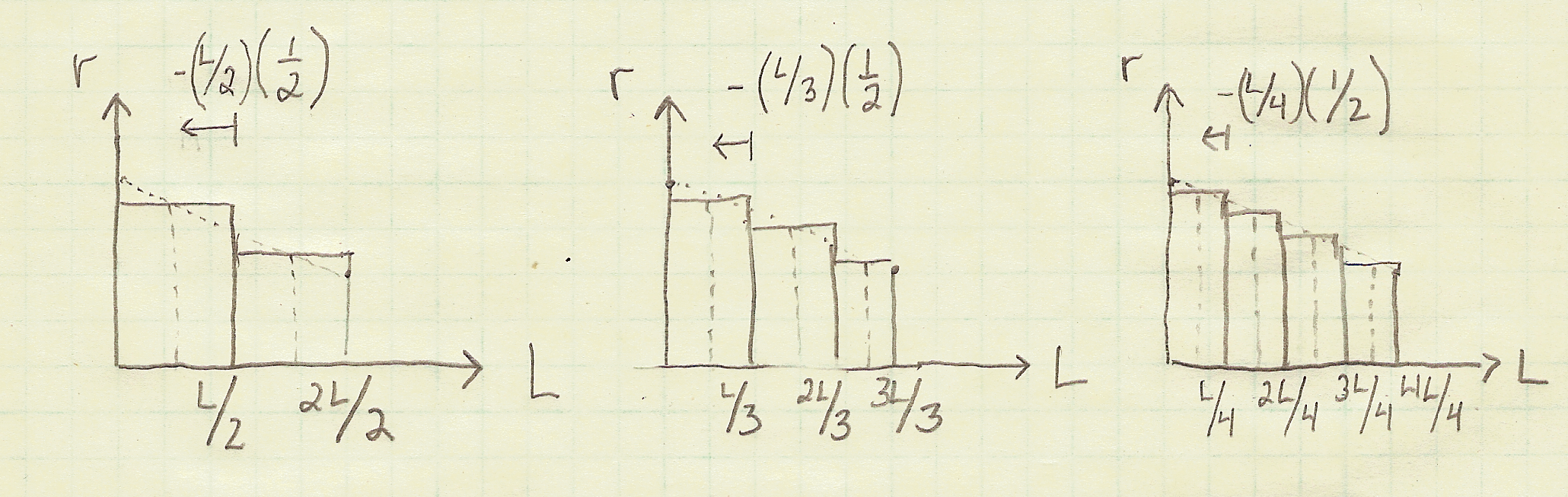
Note that as the number of disks increases, the thickness of each disk also increases.
Find the thickness of each disk¶
The thickness of each disk $L_n$ can be calculated by taking the thickness (or Length) of the entire truncated cone and dividing it by the number of disks.
$$ L_n = \frac{L}{n} $$$L_n$ = thickness of each disk
$L$ = thickness of the whole truncated cone
$n$ = number of disks the truncated cone is approximated by
Find the L value for each disk¶
Half of the disk thickness is where we will set our disk radius (the dotted vertical lines in the plot above). If we take the $L$ value (x-value) as the right-hand edge of each disk (solid vertical lines in the plot above), we need to back up half-way through the disk to set the location of the disk radius.
$$ L_i = \frac{n_i}{L} - (L_n/2) $$$L_i$ = $L$ value that's the center of disk $i$
$n_i$ = disk number
$L$ = thickness of the whole truncated cone
$L_n$ = thickness of each disk
$L_n/2$ = half the thickness of each disk (need to back up half-way through a disk to arrive at the $L$ value to set the radius)
Great! We have an equation for the $L_i$ value of each disk. However, we still need the radius $r$ of each disk to calculate the area of each disk and ultimately the deformation $\delta$ of each disk.
So what we need is an equation that spits out radius $r$ given length $L$.
Radius, r in terms of length, L¶
We can write the equation with the help of a plot. The plot below shows how radius $r$ changes based on length $L$. The relationship is a simple line that we can approximate using the form $y = mx+b$. Where $y = r$, $m = slope$, and $b = y-intercept$. The hand-drawn plot below shows the equation for our assumed values.

So our equation for $r$ in terms of $L_i$ is:
$$ r = \frac{-5}{100}L_i + 10 $$$\frac{-5}{100}$ = slope of $r$ vs. $L$
$L_i$ = L value (distance relative to the bottom of the truncated cone)
10 = y-intercept (the major radius)
Approximate truncated cone as two disks¶
Now let's use our formula for disk radius $r$ and approximate the elongation of the truncated cone using two disks ($n=2$).
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 2 # two disks
L_n = L/n # thickness of each disk
# calculate elgongation of the first disk (the disk with the larger radius)
i=1
L_1 = i*L/n-(L_n*(1/2))
print(f"L({i}) position: {L_1}")
r_1 = (-c/L)*L_1+2*c
print(f"r({i}) length: {r_1}")
A_1 = math.pi*r_1**2
d_1 = (P*L/n)/(A_1*E)
print(f"The delfection of the first disk d_1 = {d_1}")
# calculate elgongation of the second disk (the disk with the larger radius)
i=2
L_2 = i*L/n-(L_n*(1/2))
print(f"L({i}) position: {L_2}")
r_2 = (-c/L)*L_2+2*c
print(f"r({i}) length: {r_2}")
A_2 = math.pi*r_2**2
d_2 = (P*L/n)/(A_2*E)
print(f"The delfection of the second disk d_2 = {d_2}")
# add the two deflections together to calculate the total deflection
d_t = d_1 + d_2
print(f"The total estimated deflections using {n} disks is d_t = {d_t}")
Great! We can see our approximation using two disks which is about $5.13 \times 10^{-5}$ is closer to the exact value than our first approximation using one disk.
But hand coding in L_1, r_1, A_1, d_1 followed by L_2, r_2, A_2, d_2 even though we are doing the same operations each time is repetative. If we have 5 or 60 disks, we would end up with a lot of code.
Approximate truncated cone as n-disks using a for loop¶
To make our calculation work for $n$ disks, we'll use a for loop. We want to start our loop at i=1 and end our loop at i=n. We can do this with Python's range() function. Note that we set for i in range(1,n+1): (start at 1 end at n) because Python counting starts at zero and ends at n-1.
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 2 # two disks
L_n = L/n #thickness of each disk
# calculate elgongation of the first disk (the disk with the larger radius)
for i in range(1,n+1):
L_i = i*L/n-(L_n*(1/2))
print(f"L({i}) position: {L_i}")
r_i = (-c/L)*L_i+2*c
print(f"r({i}) length: {r_i}")
A_i = math.pi*r_i**2
d_i = (P*L/n)/(A_i*E)
print(f"The delfection of the disk {i} = {d_i}")
The deflection calculated using the Python for loop is the same as the deflection when we hard coded in each disk. Now we need to add these deflections together to calculate the total estimated deflection.
Sum disk deflections to find total deflection¶
We can add all of the individual disk deflections together into one variable called d_t. We'll use Python's += operator to add each disk's deflection to d_t each time we go through the for loop. The code below calculates the total deflection.
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 2 # two disks
L_n = L/n #thickness of each disk
d_t = 0
# calculate elgongation of the first disk (the disk with the larger radius)
for i in range(1,n+1):
L_i = i*L/n-(L_n*(1/2))
print(f"L({i}) position: {L_i}")
r_i = (-c/L)*L_i+2*c
print(f"r({i}) length: {r_i}")
A_i = math.pi*r_i**2
d_i = (P*L/n)/(A_i*E)
print(f"The delfection of the disk {i} = {d_i}")
d_t += d_i
print(f"The total estimated deflection using {n} disks d_t = {d_t}")
The total estimated deflection using a 2 disk approximation is $5.127 \times 10^{-5}$. This is a closer to the exact value than our estimated deflection using a 1 disk approximation.
Calculate the estimated deflection using 6, 12, and 60 disks¶
Now that the code works for 2 disks, we can easily approximate the deflection using a 6 disk, a 12 disk and a 60 disk approximation.
Approximate with 6 disks¶
The code below corresponds to a 6 disk approximation. Note how n=6 and how the variable d_6 is used to store the total deflection instead of d_t. We'll use this d_6 value later, so we want to set it to a unique variable name.
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 6 # two disks
L_n = L/n #thickness of each disk
d_6 = 0
# calculate elgongation of the first disk (the disk with the larger radius)
for i in range(1,n+1):
L_i = i*L/n-(L_n*(1/2))
print(f"L({i}) position: {L_i}")
r_i = (-c/L)*L_i+2*c
print(f"r({i}) length: {r_i}")
A_i = math.pi*r_i**2
d_i = (P*L/n)/(A_i*E)
print(f"The delfection of the disk {i} = {d_i}")
d_6 += d_i
print(f"The total estimated deflection using {n} disks d_{n} = {d_6}")
Approximate with 12 disks¶
The same code can be used to approximate the deflection using 12 disks. This time we change n=12 and change d_6 to d_12. I also commented out some of the print statements so that the output wouldn't be so long.
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 12 # twelve disks
L_n = L/n #thickness of each disk
d_12 = 0
# calculate elgongation of the first disk (the disk with the larger radius)
for i in range(1,n+1):
L_i = i*L/n-(L_n*(1/2))
#print(f"L({i}) position: {L_i}")
r_i = (-c/L)*L_i+2*c
#print(f"r({i}) length: {r_i}")
A_i = math.pi*r_i**2
d_i = (P*L/n)/(A_i*E)
print(f"The delfection of the disk {i} = {d_i}")
d_12 += d_i
print(f"The total estimated deflection using {n} disks d_{n} = {d_12}")
Using an approximation of 12 disks, we are even closer than our previous approximations.
Approximate with 60 disks¶
One more approximation to make, 60 disks. Let's comment out all of the print statements except for the final one. Remember to change n=60 and use the variable d_60.
import math
P = 10
c = 5
L = 100
E = 120*1000 #120 GPa = 120 * 1000 MPa
n = 60 # sixty disks
L_n = L/n #thickness of each disk
d_60 = 0
# calculate elgongation of the first disk (the disk with the larger radius)
for i in range(1,n+1):
L_i = i*L/n-(L_n*(1/2))
#print(f"L({i}) position: {L_i}")
r_i = (-c/L)*L_i+2*c
#print(f"r({i}) length: {r_i}")
A_i = math.pi*r_i**2
d_i = (P*L/n)/(A_i*E)
#print(f"The delfection of the disk {i} = {d_i}")
d_60 += d_i
print(f"The total estimated deflection using {n} disks d_{n} = {d_60}")
That's the closest approximation of them all. How close was each approximation? Let's quantify that using percent error.
Calculate Percent Error¶
To calculate the percent error we'll use:
$$ \%error = \frac{\delta_{approx}-\delta_{exact}}{\delta_{exact}} \times 100\% $$e_6 = (d_6-d_exact)/d_exact
print(f" The error using an approximation of 6 disks is {e_6*100}%")
e_12 = (d_12-d_exact)/d_exact
print(f" The error using an approximation of 12 disks is {e_12*100}%")
e_60 = (d_60-d_exact)/d_exact
print(f" The error using an approximation of 60 disks is {e_60*100}%")
Summary¶
In this post we calculated and estimated the deflection of a truncated cone under an applied load. We calculated the exact value of deflection using an equation. Then we used a Python for loop to estimate the truncated cone deflection by modeling the cone as a series of disks. Modeling the cone as 60 disks gave us the lowest percent error.